Silicon PhotoMultiplier (SiPM)

Publications

Basic SiPM Structure and Operation

The silicon photomultiplier is a radiation detector with extremely high sensitivity, high efficiency, and very low time jitter. It is based on reversed biased p/n diodes, it can directly detect light from near ultra violet to near infrared, and it is employed in all those applications where low light/radiation level must be measured and quantified with high precision. Light is made of photons (quantum of light). SiPMs are designed to have high gain and high detection efficiency so that even a single photon impinging on a SiPM pixel can be detected producing an output current pulse with a very low time jitter (> Rs). There are three fundamental operation modes in a GM-APD: quiescent mode, discharge phase, recovery phase. In quiescent mode, the diode is reversed biased to Vbias = Vbd +Vov (Vov is the overvoltage, i.e., the excess bias beyond Vbd). The switch in the equivalent circuit of Fig. 3 is open and unless a photon is absorbed (or a dark event occurs), the diode remains in this condition with no current flowing (neglecting leakage currents). When a photon is absorbed (or a dark event occurs), the equivalent model prescribes that the switch closes and Cd discharges from Vbias to Vbd through Rs: during this phase, avalanche multiplication is ongoing inside  

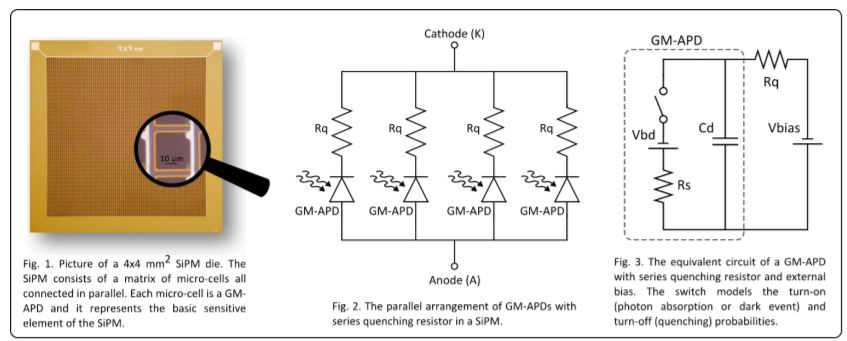
the GM-APD. Once triggered, the avalanche process is self-sustaining meaning that, without quenching, a steady current flows indefinitely in the device. With Rq, the avalanche process is quenched and the switch in the equivalent circuit of Fig. 3 opens again. The GM-APD enters now the recovery phase: Cd recharges back to Vbias through Rq and the GM-APD returns in the quiescent mode, ready for the detection of a new photon. The Cd discharge and recharge appears at the SiPM terminals as a current pulse, see Fig. 4. The rising edge corresponds to the discharge phase (time constant Cd x Rs), while the slower trailing edge is the recovery phase with time constant Cd x Rq. To mention that the quenching time is negligible. The amplitude of the SiPM pulse increases with the overvoltage while both the rising time and the recovery time are mainly determined by Cd, Rs, and Rq. During recovery, the GM-APD cannot detect other photons. For this reason, a GM-APD cannot count the number of incoming photons unless the photon rate is lower than the inverse of the recharge time. SiPMs overcomes this limitation thanks to the parallel arrangement of several micro-cells. When N photons are detected (which means that N photons arrive on N different micro-cells producing N single-cell signals) the SiPM output pulse is N-times larger than the single-cell response, in that, the N independent current pulses just add up at the SiPM terminals. To note that both the amplitude and the area of each SiPM pulse, which is the total charge delivered by the detector, are proportional to the number of detected photons (neglecting for the time being primary and correlated noise). If the number of incoming photons is larger than the number of micro-cells in the SiPM, saturation occurs and neither the amplitude nor the area of the output pulse cannot give information on the number of incoming photons anymore. In the case of not concurrent cells firing, pulses pile-up may occurs at the SiPM terminals: as an example, Fig. 6 shows three micro-cells firing in rapid sequence. As before, the area of the SiPM signal is proportional to the number of the detected photons, but it is less straightforward to retrieve information from the amplitude of

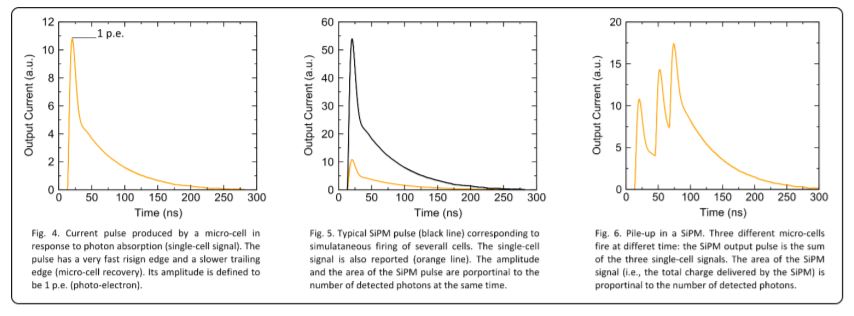
the SiPM signal. The same applies when bunches of simultaneous photons reach the SiPM surface with a certain time distribution: several pulses with different amplitude may overlap in time. SiPMs can be employed to determine the characteristics of the incoming light. For instance, when SiPMs are coupled to scintillating crystals, the SiPM output signal mimics, in time, the characteristic light emission profile of the crystal itself (under the assumption that the decay time of the crystal is much longer than the recovery time of the SiPMs and that the SiPMs works in non-saturation). In an analogue way, SiPMs are employed to evaluate also the characteristic fluorescence decay time of substances or molecules. By computing the integral of the SiPM signal one can determine the amount of charge produced by the SiPM, hence the amount of light emitted by the crystal and eventually the total energy deposited in the crystal obtaining in this way information on the type (energy) of the radiation being stopped by the crystal (i.e., spectroscopy).

Breakdown voltage

The breakdown voltage (Vbd) is the minimum (reverse) bias voltage that leads to self-sustaining avalanche multiplication in GM-APDs. In other words, it is the minimum bias for which output pulses as those shown in Fig. 4-6 can be obtained. However, for Vbias=Vbd both the detection efficiency and the gain of SiPMs are (by definition) still null. Only for Vbias > Vbd output current pulses are actually observed. The excess bias beyond the breakdown voltage is called overvoltage (Vov). By definition:

Vov = Vbias – Vbd

In principle, the higher the overvoltage, the higher the SiPM performances. In reality, since the detection efficiency tends to saturate with Vov while the noise keeps on increasing (even more than linearly) with Vov, there exist an upper limit to the optimum SiPM bias voltage. The breakdown voltage is defined by the p/n junction characteristics of the particular SiPM technology., AdvanSiD SiPMs feature Vbd in the range of 25-29 V at room temperature, and are designed to work in the overvoltage range of 2 to 5 V (refer to the SiPMs datasheets). Also the temperature dependence of the

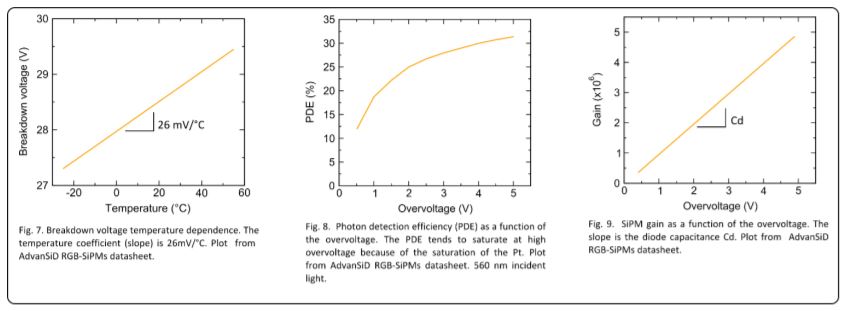
breakdown voltage is determined by the structural characteristics of the GM-APDs. An example of the Vbd temperature variation in AdvanSiD SiPMs is reported in Fig. 7. For more details, refer to [1].

Photon Detection Efficiency (PDE)

The photon detection efficiency (PDE) is the probability that a photon arriving on the SiPM surface is detected producing an output pulse. It can be defined as the ratio between the number of detected photons over the number of incoming photons. In terms of device characteristics, the PDE is defined as the product of three factors: quantum efficiency, triggering probability, and geometry efficiency:

PDE(Vov) = Qe x Pt(Vov) x FF

Quantum efficiency (Qe) expresses the probability that a photon impinging on the SiPM is actually transmitted to the silicon, absorbed in the silicon and finally converted in an electron/hole pair. Qe is a function of the wavelength and angular incidence of incoming photons. The triggering probability (Pt) is the probability that the generated electron/hole pair successfully initiates a self-sustaining avalanche process and thus an output current pulse. Pt is a strong function of the overvoltage, and it increases with Vov according to the electron and hole ionization rates dependence on the induced electric field [2]. Also Pt is wavelength-dependent since the avalanche initiation probability depends on the position inside the GM-APD where the electron/hole pair has been generated and this, in turn, depends on the wavelength of the incoming photon. The geometry efficiency (or fill-factor, FF) accounts for the fact that each micro-cell in the SiPM has necessarily some dead area on its periphery to accommodate isolating structures and metal lines for signal routing. Figure 8 shows a typical PDE curve as a function of the overvoltage. The functional dependence of PDE on overvoltage is contained in the Pt term since both Qe and FF are, for a given wavelength, constant factors. The main limiting factor in the PDE is the fill-factor: for sufficiently high overvoltage, in fact, both Qe and Pt are closed to 1 and PDE eventually saturates to FF. By definition, we have 0 < Qe, Pt, FF < 1. To maximize PDE, each of its three factors shall be optimized. Qe values as high as 0.98 are achieved by means of proper anti-reflecting coating layers deposited over the SiPM active area. Pt is maximized recurring to junction and electric field engineering [3]. Notably, AdvanSiD RGB and NUV SiPMs have different internal junction structure to maximize Pt for, respectively, visible light and near ultra violet light [3], [4]. To enhance cells fill-factor one must recur to advance lithography techniques with submicron feature size and clever device layout [5].

Gain

The gain (G) is defined as the number of carriers contained in the single-cell current pulse since this is the number of carriers generated during the avalanche in response to an absorbed photon. From Fig. 3 and relative discussion, the gain is given by the discharge of Cd from Vbias = (Vbd + Vov ) to Vbd and therefore is given by the charge stored on a capacitor of capacitance Cd with a potential difference of Vov:

G(Vov) = (Cd x Vov) / q

where q is the elementary charge. Assuming Cd constant for Vbias > Vbd, gain increases linearly with the overvoltage, see Fig. 9. Moreover, G is practically insensitive to temperature variations since Cd does not vary appreciably with temperature (within a reasonable range of temperatures). At a given bias, any gain shift with temperature has to be ascribed to the breakdown voltage shift with temperature. At an overvoltage greater than 3 V, AdvanSiD SiPMs show gain variations of less than 1%/°C thanks to the low temperature coefficient of Vbd (see Fig. 7)

Primary Noise (Dark Count Rate)

Noise in SiPMs is represented by spurious output current pulses produced in absence of light. In silicon, there is a finite probability for carriers (electron and hole) to be generated by thermal agitation. During the quiescent mode, if an electron or hole originates inside the active region of a GM-APD an avalanche is initiated (with probability Pt) and an output pulse is observed. This is called a dark event. The number of dark events per unit time is the dark count rate (DCR). In silicon photomultipliers, the thermal generation of carriers doubles approximately every 10 °C, and so does the DCR. Moreover, the DCR scales according to the SiPM area and it is an increasing function of the overvoltage. In a single GM-APD a dark event is indistinguishable from a photo-generated one. In both cases, the output pulse has 1 p.e. amplitude, see Fig. 4. In a SiPM, dark events still have 1 p.e. amplitude (neglecting direct optical crosstalk events, disused below) while the useful signal may consists of more photons impinging on the detector at the same time producing signals with amplitude greater than 1 p.e. (see also Fig. 5). In this case, a threshold can be set to, e.g., 1.5 p.e. to discard the dark events. The DCR of a SiPM should be specified for a given SiPM size, micro-cell size, overvoltage and temperature. Since the primary noise scales with the silicon area, for a given SiPM technology, the DCR can be given as Hz (or cps) per unit area, with overvoltage and temperature always specified. In some cases, it could be useful to have the DCR specified for a certain PDE rather than a certain overvoltage.

Correlated Noise: Afterpulsing, Optical Crosstalk, ECF

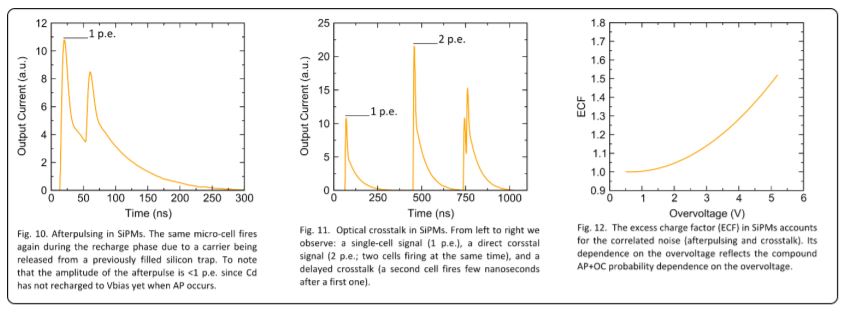
Besides the primary noise, in SiPMs there are other two sources of noise, i.e., afterpulsing (AP) and optical crosstalk (OC). Both AP and OC events originate from an existing current pulse (which can be either a photonevent or a dark-event) and for this reasons they are referred as to correlated noise. The probability of having an AP or OC event strongly depends on the current density in the original avalanche and on the triggering probability Pt. Large micro-cells have large gain, hence a high number of carriers flowing during the avalanche and thus high AP and OC probability. To contain the correlated noise it is essential to implement SiPMs with small micro-cells [6]. Afterpulsing is due to the carriers trapped in silicon defects during the avalanche multiplication that are released later on during the recharge phase of the GM-APD.

The net effect is that we observed a new current pulse on the tail of the original current pulse, see Fig. 10. AP probability increases more than linearly with the overvoltage and quadratically with the cell size because of the corresponding increase in the gain. Optical crosstalk involves photons emitted during avalanche multiplication and that are re-absorbed in neighboring cells or even in the inactive region of the same cell and causing additional current pulses. Direct OC occurs when an emitted photon reaches the active region of another cell triggering an additional avalanche practically at the same instant of the original avalanche (consider the speed of light in silicon and the very rapid avalanche ignition in GM-APDs). The result is the double pulse in Fig. 11. Delayed-OC involves, instead, photons that are re- absorbed in the inactive regions of the SiPM. The generated electron (or hole) must then diffuse to the active region of a cell before being able to trigger an avalanche. The correlated pulse has therefore a certain time-delay (in the order of few ns) with respect to the original one, see the third signal in Fig. 11. As for AP, in first approximation OP probability increases more than linearly with the overvoltage and quadratically with the cell size. For a more exhaustive treatment of optical crosstalk in SiPMs refer to [7]. The effect of both AP and OC is to produce additional charge with respect to the charge associated to an original SiPM pulse (photon-event or a dark-event). The SiPM dark current (reverse bias IV characteristics, Vov > 0) is given by the charge due to primary dark pulses plus the charge due to AP and OC pulses. If we assume no AP and no OC then the SiPM dark current at a given Vov consists of the charge due to primary dark pulses only:

Idark_ideal(Vov) = q x GAIN(Vov) x DCR(Vov)

This is an “ideal” current since in practice there is always a contribution due to AP an OC events. The contribution of AP and OC to the SiPM dark current can be modeled with an additional term to the ideal SiPM dark current called excess charge factor (ECF):

Idark_real(Vov) = q x GAIN(Vov) x DCR(Vov) x ECF

Since both Idark_real(Vov) and DCR(Vov) can be accurately measured in laboratory, it is possible to quantify the ECF as

ECF(Vov) = Idark_real(Vov) / Idark_ideal(Vov)

Fig. 12 reports a typical plot of the ECF as a function of the overvoltage. By definition, in absence of AP and OC, ECF is one. At low overvoltage, AP and OC probabilities are very low and ECF is closed to 1.

References

[1] N. Serra, G. Giacomini, A. Piazza, C. Piemonte, A. Tarolli, N. Zorzi, Experimental and TCAD Study of Breakdown Voltage Temperature Behavior in n+/p SiPMs, in «IEEE TRANSACTIONS ON NUCLEAR SCIENCE», vol. 58, n. 3, 2011, pp. 1233 – 1240

[2] S. Sze and K. Ng, Physics of Semiconductor Devices, 3rd ed. Hoboken, NJ: Wiley-Interscience, 2006.

[3] N. Serra, A. Ferri, A. Gola, T. Pro, A. Tarolli, N. Zorzi, C. Piemonte, Characterization of new FBK SiPM technology for visible light detection, in «JOURNAL OF INSTRUMENTATION», vol. 8, n. P03019, 2013

[4] T. Pro, A. Ferri, A. Gola, N. Serra, A. Tarolli, N. Zorzi, C. Piemonte, New Developments of Near-UV SiPMs at FBK, in «IEEE TRANSACTIONS ON NUCLEAR SCIENCE», vol. 60, n. 3, 2013 , pp. 2247 – 2253

[5] C. Piemonte, A. Ferri, A. Gola, T. Pro, N. Serra, A. Tarolli, N. Zorzi, Characterization of the First FBK HighDensity Cell Silicon Photomultiplier Technology, in «IEEE TRANSACTIONS ON ELECTRON DEVICES», vol. 60, n. 8, 2013, pp. 2567 – 2573

[6] C. Piemonte, A. Ferri, A. Gola, A. Picciotto, T. Pro, N. Serra, A. Tarolli, N. Zorzi, Development of an automatic procedure for the characterization of silicon photomultipliers, Conference Record of NSS/MIC 2012, IEEE, 2012, pp. 428-432

[7] A. Gola, A. Tarolli, C. Piemonte, SiPM Cross-talk Amplification due to Scintillator Crystal: Effects on Timing Performance, Conference Record of NSS/MIC 2012, IEEE, 2012 , pp. 421-423